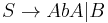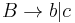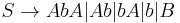Chomsky normal form
In formal language theory, a context-free grammar is said to be in Chomsky normal form if all of its production rules are of the form:
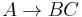 or
or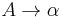 or
or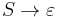
where  ,
,  and
and  are nonterminal symbols, α is a terminal symbol (a symbol that represents a constant value),
are nonterminal symbols, α is a terminal symbol (a symbol that represents a constant value),  is the start symbol, and ε is the empty string. Also, neither
is the start symbol, and ε is the empty string. Also, neither  nor
nor  may be the start symbol.
may be the start symbol.
Every grammar in Chomsky normal form is context-free, and conversely, every context-free grammar can be transformed into an equivalent one which is in Chomsky normal form. Several algorithms for performing such a transformation are known. Transformations are described in most textbooks on automata theory, such as (Hopcroft and Ullman, 1979). As pointed out by Lange and Leiß, the drawback of these transformations is that they can lead to an undesirable bloat in grammar size. The size of a grammar is the sum of the sizes of its production rules, where the size of a rule is one plus the length of its right-hand side. Using 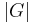 to denote the size of the original grammar
to denote the size of the original grammar  , the size blow-up in the worst case may range from
, the size blow-up in the worst case may range from 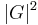 to
to 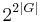 , depending on the transformation algorithm used (Lange and Leiß, 2009).
, depending on the transformation algorithm used (Lange and Leiß, 2009).
Contents |
Alternative definition
Another way to define Chomsky normal form (e.g., Hopcroft and Ullman 1979, and Hopcroft et al. 2006) is:
A formal grammar is in Chomsky reduced form if all of its production rules are of the form:
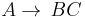 or
or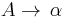
where  ,
,  and
and  are nonterminal symbols, and α is a terminal symbol. When using this definition,
are nonterminal symbols, and α is a terminal symbol. When using this definition,  or
or  may be the start symbol. Only those context-free grammars which do not generate the empty string, can be transformed into Chomsky reduced form.
may be the start symbol. Only those context-free grammars which do not generate the empty string, can be transformed into Chomsky reduced form.
Converting a grammar to Chomsky Normal Form
- Introduce
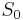
- Introduce a new start variable,
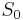 and a new rule
and a new rule 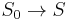 where
where  is the previous start variable.
is the previous start variable.
- Introduce a new start variable,
- Eliminate all
 rules
rules
 rules are rules of the form
rules are rules of the form 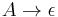 where
where 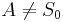 and
and 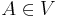 where
where  is the CFG's variable alphabet.
is the CFG's variable alphabet.- Remove every rule with
 on its right hand side (RHS). For each rule with
on its right hand side (RHS). For each rule with  in its RHS, add a set of new rules consisting of the different possible combinations of
in its RHS, add a set of new rules consisting of the different possible combinations of  replaced or not replaced with
replaced or not replaced with  . If a rule has
. If a rule has  as a singleton on its RHS, add a new rule
as a singleton on its RHS, add a new rule 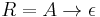 unless
unless  has already been removed through this process. For example, examine the following grammar
has already been removed through this process. For example, examine the following grammar  :
:
 has one
has one  rule. When the
rule. When the 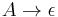 is removed, we get the following:
is removed, we get the following:
- Notice that we have to account for all possibilities of
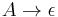 and so we actually end up adding 3 rules.
and so we actually end up adding 3 rules.
- Eliminate all unit rules
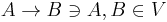
- After all the
 rules have been removed, you can begin removing unit rules, or rules whose RHS contains one variable and no terminals (which is inconsistent with CNF).
rules have been removed, you can begin removing unit rules, or rules whose RHS contains one variable and no terminals (which is inconsistent with CNF).
- To remove
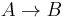
 add rule
add rule 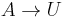 unless this is a unit rule which has already been removed.
unless this is a unit rule which has already been removed.
- To remove
- Clean up remaining rules that are not in Chomsky normal form.
- Replace Failed to parse (unknown function\dotso): A \rightarrow u_1 u_2 \dotso u_k, k \ge 3, u_1 \in V \cup \Sigma
with Failed to parse (unknown function\dotsc): A \rightarrow u_1 A_1 , A_1 \rightarrow u_2 A_2 , \dotsc , A_{k-2} \rightarrow u_{k-1} u_k
where 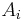 are new variables.
are new variables.
-
- If
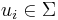 , replace
, replace 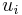 in above rules with some new variable
in above rules with some new variable 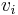 and add rule
and add rule 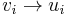 .
.
- If
See also
References
- John E. Hopcroft, Rajeev Motwani, and Jeffrey D. Ullman. Introduction to Automata Theory, Languages, and Computation, 3rd Edition, Addison-Wesley, 2006. ISBN 0-321-45536-3. (See subsection 7.1.5, page 272.)
- John E. Hopcroft and Jeffrey D. Ullman, Introduction to Automata Theory, Languages and Computation, Addison-Wesley Publishing, Reading Massachusetts, 1979. ISBN 0-201-02988-X. (See chapter 4.)
- Michael Sipser (1997). Introduction to the Theory of Computation. PWS Publishing. ISBN 0-534-94728-X. (Pages 98–101 of section 2.1: context-free grammars. Page 156.)
- John Martin (2003). Introduction to Languages and the Theory of Computation. McGraw Hill. ISBN 0-07-232200-4. (Pages 237–240 of section 6.6: simplified forms and normal forms.)
- Michael A. Harrison (1978). Introduction to Formal Language Theory. Addison-Wesley. ISBN 978-0201029550. (Pages 103–106.)
- Lange, Martin and Leiß, Hans. To CNF or not to CNF? An Efficient Yet Presentable Version of the CYK Algorithm. Informatica Didactica 8, 2009. ((pdf)
- Cole, Richard. Converting CFGs to CNF (Chomsky Normal Form), October 17, 2007. (pdf)
- Sipser, Michael. Introduction to the Theory of Computation, 2nd edition.